MATH MATTERS: A REVIEW OF CALCULATIONS FOR NONSTERILE COMPOUNDING
Liz Fredrickson, PharmD, BCPS
Liz Fredrickson is an Associate Professor of Pharmacy Practice and Pharmaceutical Sciences at the Northeast Ohio Medical University College of Pharmacy. She serves as Director of Instructional Labs and is course director for the Basic Pharmaceutics Lab and Parenteral Products and Parenteral Products Lab courses.
Topic Overview
A strong understanding of pharmaceutical calculations provides pharmacy technicians and pharmacists the ability to prepare compounded nonsterile preparations accurately and safely. This course provides an overview of fundamental pharmaceutical calculations, including units of measurement, conversions, the ratio and proportion method, dimensional analysis, expressions of concentrations, density, and specific gravity. The alligation and aliquot methods will be reviewed, as well as calculations related to drug dosing and reconstitution. Step-by-step example problems will be provided to aid the learner in understanding these concepts.
Accreditation Statement:

RxCe.com LLC is accredited by the Accreditation Council for Pharmacy Education (ACPE) as a provider of continuing pharmacy education.
Universal Activity Number (UAN): The ACPE Universal Activity Number assigned to this activity is
Pharmacist 0669-0000-23-178-H07-P
Pharmacy Technician 0669-0000-23-179-H07-T
Credits: 2 hours of continuing education credit
Type of Activity: Application
Media: Internet/Home study Fee Information: $6.99
Estimated time to complete activity: 2 hours, including Course Test and course evaluation
Release Date: October 21, 2023 Expiration Date: October 21, 2026
Target Audience: This educational activity is for pharmacists.
How to Earn Credit: From October 21, 2023, through October 21, 2026, participants must:
Read the “learning objectives” and “author and planning team disclosures;”
Study the section entitled “educational activity;” and
Complete the Course Test and Evaluation form. The Course Test will be graded automatically. Following successful completion of the Course Test with a score of 70% or higher, a statement of participation will be made available immediately. (No partial credit will be given.)
Credit for this course will be uploaded to CPE Monitor®.
Learning Objectives: Upon completion of this educational activity, participants should be able to:
Convert units of measurement
Recognize methods used to solve calculations for nonsterile compounding
Perform calculations necessary to prepare compounded nonsterile preparations
Disclosures
The following individuals were involved in developing this activity: Liz Fredrickson, PharmD, BCPS, and Pamela Sardo, PharmD, BS. Pamela Sardo was an employee of Rhythm Pharmaceuticals until March 2022 and has no conflicts of interest or relationships regarding the subject matter discussed. There are no financial relationships relevant to this activity to report or disclose by any of the individuals involved in the development of this activity.
© RxCe.com LLC 2023: All rights reserved. No reproduction of all or part of any content herein is allowed without the prior, written permission of RxCe.com LLC.
Introduction
Preparing a compounded nonsterile preparation (CNSP) requires the successful completion of many steps, including accurately weighing ingredients, compounding the preparation, labeling the preparation, and documenting the process. One key component is completing pharmaceutical calculations. This allows compounding personnel to calculate doses, adjust formulas, and determine the correct quantities of ingredients to be weighed and measured. Within USP <795> Pharmaceutical Compounding - Nonsterile Preparations, the ability to complete calculations accurately is a requirement of both compounding personnel and those directly overseeing compounding personnel.1
Errors in calculations can have potentially devastating consequences, including major patient harm or death. Thus, the goal in completing calculations should be one hundred percent accuracy. If not, patients may receive a subtherapeutic preparation and derive no little or no benefit.2 Conversely, the preparation could be supratherapeutic, resulting in adverse events or toxicities.2
This course will provide an overview of fundamental pharmaceutical calculations and related concepts, including units of measure, conversions, the ratio and proportion method, dimensional analysis, expressions of concentrations, density, and specific gravity. The alligation and aliquot methods will be reviewed, as well asl calculations related to drug dosing and reconstitution. Step-by-step example problems will be provided to aid the learner in understanding these concepts.
Calculation Considerations
Prior to solving pharmaceutical calculations, compounding personnel should establish a standardized process. The following questions can be used to guide this process:2
What is the goal of this problem?
What mathematical process(es) is/are needed to solve this problem?
How can I correctly complete those processes?
Solving calculations involves thoroughly reviewing the prescription and formula used to compound the prescription. If there are errors within the prescription, these will need to be addressed. Once these documents have been reviewed, the next step is to organize all information necessary to complete calculations. This could include the patient’s weight, the density or specific gravity values of ingredients, or the quantity of medication requested by the prescription.
There are often many ways to solve pharmaceutical calculations. While it is beneficial to be familiar with the various methods by which to solve a problem, it is best to use a method that is comfortable and familiar. It is also very important to double-check your work or have a colleague check your work prior to compounding the prescription. When solving calculations, it is best practice to use as few steps as possible.2 The more steps involved, the more likely a mathematical error will occur. It is also helpful to approximate the correct answer before completing the calculation.2 This gives you an estimate with which to compare your actual answer. For example, you can determine if your answer is higher or lower than anticipated and recognize a mistake before compounding the preparation. Finally, the best way to become skillful at solving calculations is to practice! The more you review and study these concepts, the more skilled you will become.
Systems of Measurement
Within the process of nonsterile compounding, quantities of ingredients (volumes or weights) can be expressed using various measurement systems. For compounding personnel, it is essential to understand these systems and how to convert between them. There are four main systems of measurement. These include:
The metric system
The apothecaries’ system
The avoirdupois system
The household system
The Metric System
The metric system is the most utilized measurement system within pharmaceutical compounding, and it is also the preferred system of measurement within the practice of pharmacy.3 Metric units of weight and volume are commonly utilized to determine drug dosages and drug strengths within nonsterile compounding.2 The metric system is based on the decimal system, in which measurements are made in multiples (or fractions) of 10. The metric system includes three base units:3 gram for weight, liter for volume, and meter for length.
Prefixes are used to denote ingredient quantities that are either larger or smaller than these base units.2,3 These prefixes are defined in Table 1. Compounding personnel will commonly need to adjust between units of the metric system. Understanding these prefixes allows compounding personnel to adjust from one denomination to another easily.
Table 1. Metric System Prefixes
| Prefix | Meaning |
| mega- | one million times the base unit (106) |
| kilo- | one thousand times the base unit (103) |
| deci- | one-tenth the base unit (10-1) |
| centi- | one-hundredth the base unit (10-2) |
| milli- | one-thousandth the base unit (10-3) |
| micro- | one-millionth the base unit (10-6) |
| nano- | one-billionth the base unit (10-9) |
Converting from one denomination to another is simple process that involves moving the decimal point either to the left or right. For example, to convert from liters to milliliters, you would move the decimal point three places to the right. Doing so signifies multiplying by 1000.3 Another important point is that when adding, subtracting, multiplying, or dividing, you must
make sure all values have the same units.3 A value in grams cannot be added to a value in milligrams without first converting to the same denomination.3 For example, you cannot add 100 mg to 1 g. Instead, you could convert 1 gram to 1000 mg and then add 100 mg + 1000 mg to get a total of 1100 mg.
Example: Convert from 500 milligrams (mg) to grams (g).
To convert from milligrams to grams, recall that 1 gram is equal to 1000 mg. This calculation then involves moving the decimal point to the left (or dividing by 1000). Knowing this, we can set up the following calculation:
500 mg x 1 g/1000 mg = x
Milligrams cancel, leaving the desired units of grams in the final answer: 500 mg x 1 g/1000 mg = x
x = 0.50 grams The Apothecary System
Historically, the apothecary system was more widely utilized than it is today. However, its use persists among some healthcare professionals, so being able to convert between the apothecary system and metric system is helpful for compounding personnel.2 Within this system, the base unit of measure for weight is the grain.2,3 One grain is equivalent to 65 milligrams.2 Common units of measure for volume include the fluid ounce, gallon, quart, and pint.2,3
The Avoirdupois System
The avoirdupois system is used for measurements of weight, most commonly in the context of bulk or stock packages of drugs.2,3 Within the avoirdupois system, the grain is the basic unit of measurement.3 Other common units of measurement include the pound and ounce.3
The Household System
A final system of measurement is known as the household system. This is commonly utilized when measuring liquid dosage forms, such as suspensions and solutions.2 Prescribers may refer to units of measurement such as tablespoon and teaspoon when prescribing liquid medications. Because of this, the use of the household system may lead to errors in drug dosing, as patients will sometimes use measuring devices (such as soup spoons) that are not calibrated. It is best practice to dispense a calibrated measuring device (such as a syringe) with liquid compounded preparations to avoid dosing errors.2
Common Units of Measure
Table 2 details common units of weight, and Table 3 details common units of volume.
Table 2. Units of Weight
| Unit | Abbreviation | System |
| gram | g | metric |
| milligram | mg | metric |
| kilogram | kg | metric |
| microgram | ug or mcg | metric |
| ounce | oz | avoirdupois |
| pound | lb | avoirdupois |
| grain | gr | avoirdupois/apothecary |
Table 3. Units of Volume
| Unit | Abbreviation | System |
| teaspoon | tsp or t | household |
| tablespoon | tbsp or T | household |
| fluid ounce | fl oz | apothecary |
| gallon | gal | apothecary |
| quart | qt | apothecary |
| pint | pt | apothecary |
| milliliter | mL | metric |
| liter | L | metric |
Converting Between Units
While the metric system is most utilized, there may be times when compounding personnel need to convert from one system to another, establishing equivalencies between systems.2 Below are common conversions for weight- and volume-based measurements.
Common Conversions: Weight
1 gram = 1000 mg
1 milligram = 1000 mg
1 kg = 1000 g
1 kilogram = 2.2 lbs
1 pound = 454 g
1 pound = 16 oz
1 ounce = 28.35 g
1 ounce = 437.5 gr
1 grain = 64.8 mg
The following are common conversions for volume measurements.
Common Conversions: Volume
1 tsp = 5 mL
1 tbsp = 15 mL
1 fl oz = 29.57 mL
1 gal = 3,785 mL
1 gal = 4 qt
1 qt = 2 pt
1 pt = 473 mL
1 gal = 128 fl oz
1 liter = 1000 mL
Example: How many fluid ounces are in 1 gallon? Reference the above information to recognize that 1 gallon is equivalent to 128 fluid ounces.
Choose Your Own Adventure: Ratios and Proportion Method and Dimensional Analysis
Ratios and Proportions
The ratio and proportion method is a common strategy to solve for an unknown variable when three other variables are known.2,3 Ratios and proportions offer useful ways to set up organized calculations.2 To understand this method, let’s first discuss the concepts of ratios and proportions. A ratio is defined as a comparison of two or more numbers that indicate their size in relation to each other.2,3 In a basic sense, a ratio is a relationship between two values.2 Ratios can be written several ways, including as a quotient, fraction, percentage, or decimal.3 For example, if we were discussing the ratio of 3 to 5, we could write this as 3:5 or 3/5, 0.6 or 60%.
The fraction form is commonly used when drug concentrations are expressed (for example, 10 mg/mL).2,3 However, it is important to recognize that if the ratio is written as a fraction, this should not be read as a fraction.
Using our example above, 3/5 does not mean “three-fifths” but rather “3 to 5.”
A proportion is defined as two ratios that are set equal.2,3 Proportions are the practical application of ratios and are useful when two properties are directly related.2,3 Like ratios, you may see proportions written in several different ways, including the following:
a/b = c/d a:b = c:d a:b::c:d
Using our example of 3 to 5 above, we could write this as follows: 3/5 = 6/10
3:5 = 6:10
3:5::6:10
This is read as 3 is to 5 as 6 is to 10.
When setting up a proportion, it is very important that the numbers in the numerator (numbers on top) and the numbers in the denominator (numbers on bottom) match. In other words, expressions on opposite sides of the equal sign should have the same units.3 If these are switched, mathematical errors will result. To help avoid errors, you should always write the corresponding units of all values within a calculation. For example, consider the following problem. If 4 mg of drug are contained in every 5 mL of solution, how many milligrams of drug are contained in 10 mL of solution? To avoid confusion, instead of setting up the proportion as follows:
4/5 = x/10
It should be set up like this: 4 mg/5 mL = x mg/10 mL
Example: If 20 g of an ointment contains 5 mg of active ingredient (API), how many milligrams of the active ingredient will be contained in 35 g of the ointment?
Begin this problem by setting up a proportion: 5 mg API/20 g ointment
= x mg API/35 g ointment
You can then cross-multiply and divide to isolate and solve for “x”: 5 mg (35 g) = x mg (20 g)
x mg = (5 mg x 35 g)/20 g x = 8.75 mg
Check your work!
If 20 grams contains 5 mg and 35 grams is larger than 20, then our answer should be larger than 5 mg. Thirty-five is almost double 20, so our answer should be approximately five doubled, or close to ten.
Dimensional Analysis
A second method to solve for an unknown variable is known as dimensional analysis. This involves creating relationships between quantities, such that all units cancel except for the desired units.2,3 Dimensional analysis allows for the use of one single calculation, compared to the multiple steps involved in the ratio and proportion method.2,3 This is also a useful method when you must convert between different units of measurement.2 To set up a dimensional analysis equation, the following steps can be used:2
Write out the desired unit(s) you need to obtain, followed by an equal sign
Identify a relationship between the information in your problem that contains the units you need for your answer. Include a unit with every number.
Connect the relationships, inverting dimensions as needed, and add known conversions so units will cancel.
Solve the problem mathematically
At times, a direct conversion may not be possible, and an intermediate conversion may need to be included.2 For example, to go from feet to meters, you may first need to convert from feet to inches and then from inches to centimeters then centimeters to meters.
Example: A patient will take 5 mg/kg/day of a drug each day. How many milliliters of a 20 mL vial containing 100 mg/mL should be administered to this patient if they weigh 150 lb? To solve this problem, we need to determine the intended units for our answer, which are milliliters. We can then proceed through the remaining steps. Part of this problem involves recognizing that 1 kg is equal to 2.2 lbs.
? milliliters = 1 mL/100 mg x 5 mg/kg/day x 1 kg/2.2 lbs x 150 lbs =3.4 mL
Compounding personnel should be familiar with the ratio and proportion method and dimensional analysis but can utilize whichever method is more familiar and comfortable.
Drug Dosing Calculations
A key part of determining the accuracy of a nonsterile compound prescription is checking to make sure a reasonable and accurate dose was prescribed for the patient. Doses can be determined in many ways, including based on a patient’s weight, body surface area, or age.2
In completing these calculations, there are three key considerations for pharmacy personnel:2
The size of the dose
The number of doses prescribed
The total quantity of drug
The following equation can be used to calculate number of doses:
Number of doses = total amount of drug/size of the dose2
If compounding personnel have two of these three variables, they can calculate the third. The equation can be rearranged as follows:
Number of doses = total quantity/size of dose
Total quantity = (number of doses) x (size of dose)
Size of dose = total quantity/number of doses
Example: If the dose of a drug is 100 mg, how many doses are contained in 6 g?
Before solving this problem, we will need to convert 6 grams to milligrams:
6 g x 1000 mg/1 g= 6000 mg
Use the following equation to then solve for the number of doses:
Number of doses = total quantity/size of dose Number of doses = 6000 mg/100 mg = 60 doses
Drug Concentration Expressions
Concentration
Concentration is an expression of the ratio of the amount of an ingredient to the amount of total product.3 Depending on the formula, this could be expressed as a percentage strength or ratio strength.2 Concentration is a very useful concept when determining quantities of ingredients needed for a nonsterile preparation. The following two equations can be used to either solve for concentration or the quantity of solute.3
Concentration = quantity of solute (or drug)/quantity of preparation
Quantity of solute (or drug) = concentration x quantity of preparation
Percent
A percent is simply defined as the number of parts in 100. You may see percent written as either a decimal or a fraction. For example, fifty percent can be noted as:
50% = 0.50 = 50/100
Percentage strength is an important concept when preparing CNSPs.2,3 Percentage strength is the number of parts of solute or drug in 100 units of solution or total mixture.2,3 You may see percentage strength expressed in three different ways, including the following:
Percent weight-in-weight: the number of grams of solute or drug in 100 grams of total weight (solute + diluent) of the preparation2
For example: 2% w/w = 2 grams/100 grams
Percent weight-in-volume: the number of grams of solute or drug in 100 mL of the total volume (solute and solvent) of the preparation.
For example: 2% w/v = 2 grams/100 mL
Percent volume-in-volume: the number of milliliters of solute or drug in 100 mL of the total volume (solute and solvent) of the preparation.
For example: 2% v/v = 2 gram/100 mL
Example: If 100 grams of an ointment contains 25 grams of a drug substance, what is the percent strength of the preparation?
Use the ratio and proportion method to solve:
100 grams/25 grams = 100%/x% x = 25%
Example: What quantity of drug would be present in 250 mL of a 5% w/v solution?
To solve this problem, first recognize that 5% w/v means 5 g in 100 mL. Now, use the concentration equation to solve for the quantity of the drug in grams:
Quantity of solute= concentration x quantity of preparation Quantity of solute = 5 g/100 mL x 250 mL
Quantity of solute = 12.5 g Check it Out!
If 5% w/v means 5 g in 100 mL, the quantity of the drug in 250 mL should be larger than 5 g, given that 250 mL is larger than 100 mL. If our answer was less than 5 g, we would have to check to see where an error was made.
Example: A cream contains 1% hydrocortisone. How many grams of hydrocortisone would be needed to prepare a 30-gram tube of this cream?
To solve, recognize that 1% hydrocortisone means 1 g of hydrocortisone in 100 grams of cream. Then use the concentration equation to solve for the quantity of hydrocortisone needed:
Quantity of hydrocortisone = concentration x quantity of preparation
Quantity of hydrocortisone = 1 g/100 g x 30 g Quantity of hydrocortisone = 0.3 g of hydrocortisone
Ratio Strength
Ratio strength is another way to express concentration. This is an alternative method to percentage strength in which drug concentrations are expressed in terms of a ratio.2,3 Ratio strength is written as 1 unit of solute (or drug) in the total amount of the solution (or mixture) and the numbers are read as parts.2,3 For example: 1:200 would be read as 1 part in 200 parts. Ratio strength uses the same units as percentage strength. The second number in the ratio is always the total quantity of the mixture.2,3
Ratio volume-in-volume: this represents a liquid in a liquid (units: mL in mL)
Example: 1:100 solution means 1 mL in 10 mL
Ratio weight-in-volume: this represents a solid in a liquid (units: g in mL) Example: 1:100 preparation means 1 g in 100 mL
Ratio weight-in-weight: this represents a solid in a solid (units: g in g) Example: 1:100 preparation means 1 g in 100 g
Example: Express 0.05% as a ratio strength.
To solve, recognize that 0.05% is equal to 0.05/100. Then, use the ratio and proportion method:
Set up a proportion: 0.05/100 = 1/x parts
Cross-multiply: 0.05 x (x parts) = 100
Divide and solve for x: x = (100/0.05) x = 2000 so the ratio strength is 1:2000
Example: What is the percentage strength of a 1:3000 w/v solution?
To solve, use the ratio and proportion method:
Set up a proportion: 1/3000 = x/100
Cross-multiply: 3000(x) = 100 (1)
Divide and solve for x: x = 100/3000
x = 0.033 so the percentage strength is 0.033% w/v
Density and Specific Gravity
During the compounding process, there are many times when personnel need to convert a liquid measurement to a weight measurement or a weight measurement to a liquid measurement. Some formulas list all ingredients by weight, including liquid ingredients. Density and specific gravity are useful for interconverting between volumes and weights.2,3 Depending on the reference, specific gravity may be listed instead of density.2,3
Density (d) is defined as mass per unit volume (M/V) of a particular substance and normally has units of g/mL.2 Specific gravity (sp gr) is defined as the ratio of the density of a substance to the density of a reference material.3 Water has a specific gravity of 1 (1 g water = 1 mL water) and is used as the standard for specific gravities of liquids and solids.3
The following equation is useful for specific gravity calculations:2 Grams = Milliliters x Specific Gravity
Example: What is the weight (in grams) of 3 fluid ounces of a liquid that has a specific gravity of 2.1?
To solve this problem, first convert from fluid ounces to milliliters: 3 fl oz x 29.57 mL/fl oz = 88.71 mL
Next, multiply this volume by the specific gravity of the liquid to determine weight in grams:
Grams = Milliliters x Specific Gravity Grams = 88.71 mL x 2.1
= 186.3 grams
Example: If 10 glycerin suppositories are made using the formula below, how many milliliters of glycerin would be needed to prepare 50 suppositories? The specific gravity of glycerin is 1.25.
Glycerin 91 g Sodium stearate 9 g Purified water 5 g
To solve, determine the quantity of glycerin needed to make 50 suppositories. Using the ratio and proportion method:
91 g/10 suppositories = x g/50 suppositories x = 455 grams is required
Next, divide grams of glycerin by its specific gravity to determine milliliters needed:
Milliliters = Grams/Specific Gravity 455 g/1.25 = 364 mL
Calculations for Weighing
Accurately weighing ingredients is a critical component of nonsterile compounding. The aliquot method of weighing can be used when the degree of precision desired is beyond the capacity of the weighing instrument (balance or scale).2
Least Weighable Quantity
The Least Weighable Quantity (LWQ) is the smallest quantity that can be weighed on a balance of known sensitivity to maintain a desired level of accuracy.2 Essentially, the LWQ is the minimum quantity at your facility that you are permitted to measure, based on your facility’s desired level of accuracy and the sensitivity requirement of your balance.2 To solve for LWQ, we need to know a few things. First is the sensitivity requirement (SR), which must be 6 mg or less for a Class A prescription balance. You also need to know the percent error, which is the error tolerance allowed at your facility.2 This could be anywhere from 0 to 5 percent.
The LWQ can be determined as follows:
LWQ = sensitivity requirement/%error tolerated x 100% The equation can also be rearranged to solve for %error
%error = sensitivity requirement/quantity weighed x 100%
Example: Calculate the least weighable quantity (LWQ) that will result in an error less than or equal to 5% on a balance with a sensitivity requirement of 6 mg.
To solve, plug known values into the LWQ equation:
LWQ = sensitivity requirement/%error tolerated x 100% LWQ = 6 mg/5% x 100% = 120 mg
Aliquot Method
When you need to weigh out an amount of an ingredient that is less than the LWQ, you will need some other means for weighing such a small amount of drug accurately. The aliquot method allows you to make small quantities of ingredients measurable. This method involves using an inert
diluent to increase the weight of your desired substance so an aliquot (or portion) can be accurately weighed.2,3 When using this method, the goal is to determine a weighable amount without wasting any product. The steps of the aliquot method are detailed below:3
Step 1: Calculate the LWQ for your balance or the smallest quantity that can be weighed on your balance with the desired accuracy.
Step 2: Determine the quantity of the ingredient to be weighed with the desired accuracy. To do this, multiply the quantity of the ingredient needed for the prescription by any whole number (called a factor) until a weighable quantity is achieved.
Step 3: Determine the amount of total mixture to make by multiplying the factor from Step 2 by the amount of the ingredient to be weighed.
Step 4: Determine the amount of diluent to add by subtracting the amount of ingredient to be weighed from the total amount of mixture calculated in Step 3.
Step 5: After weighing and mixing these amounts, weigh out enough of the prepared mixture to obtain an aliquot containing the desired quantity of the ingredient.
As a reminder, drug, diluent, and aliquot quantities must be greater than or equal to the LWQ.
Example: Your pharmacy receives a prescription requesting five, 5 mg morphine capsules. How can this quantity of morphine be accurately weighed using a balance with a LWQ of 120 mg?
Step 1: Calculate the LWQ for your balance.
The total quantity of morphine needed is 5 x 5 mg = 25 mg. The least weighable quantity is 120 mg.
25 mg is less than 120 mg, so the aliquot method is required.
Step 2: Determine the amount of morphine to be weighed. To do this, multiply the quantity of morphine needed by any whole number (factor) until a weighable quantity is achieved.
25 mg x 5 = 125 mg
If you are unsure which factor to pick, you can start by multiplying the quantity by 1 and proceeding until the resulting value is at or greater than your LWQ:
25 mg x 1 = 50 mg
25 mg x 2 = 100 mg
25 mg x 3 = 150 mg
25 mg x 4 = 100 mg
25 mg x 5 = 125 mg
Step 3: Determine the amount of total mixture to make by multiplying the factor from Step 2 by the amount of morphine to be weighed.
125 mg x 5 = 625 mg
Step 4: Determine the amount of diluent to add by subtracting the amount of morphine to be weighed from the total amount of mixture calculated in Step 3.
625 mg (total mixture) – 125 mg (morphine) = 500 mg (diluent)
Step 5: Weigh out enough of the prepared mixture to obtain the aliquot containing 25 mg of morphine. This can be determined using the ratio and proportion method. You can also divide the quantity of the total mixture by your factor.
125 mg morphine/625 mg mixture = 25 mg morphine/x mg mixture or
625 mg/5 = x = 125 mg
125 mg of the mixture contains 25 mg of morphine
Alligation Method
The alligation method can be used to determine a new strength of a preparation that is between two strengths of preparation you have available in the pharmacy.2,3 This method determines how many parts of each strength should be mixed. The new preparation strength will be between the two strengths used.2,3
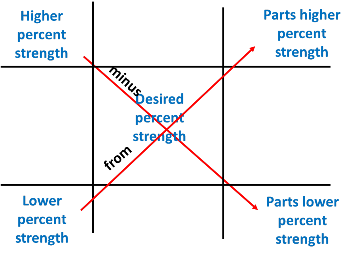
This type of problem can be set up by first drawing a “tic tac toe” board as shown below.
Next, values are placed as follows, using the “high goes high, low goes low” mnemonic. The higher percent strength value goes into the upper left corner of the board. The lower percent strength value goes into the lower left corner of the board. The desired strength goes into the middle of the board. Once these values are placed, the desired strength is subtracted from the higher percent strength, with the result placed into the lower right corner of the board. This value represents the parts of the lower percent strength preparation needed. Next, the lower percent strength is subtracted from the desired percent strength, with the resulting value placed in the upper right corner. This value represents the parts of the higher percent strength preparation needed. The two values on the right can be added to provide the total parts needed to compound the prescription.

Example: The pharmacy needs to compound a batch of 3.75% zinc oxide ointment starting from a batch of 10% zinc oxide ointment. How many grams of ointment base and 10% zinc oxide ointment should be mixed to make 120 grams of a 3.75% zinc oxide ointment?
To solve this, start by drawing a “tic tac toe” board.
Next, place your known and desired values. 10% is the higher percent strength, 0 is the lower percent strength, and 3.75% is the desired percent strength.

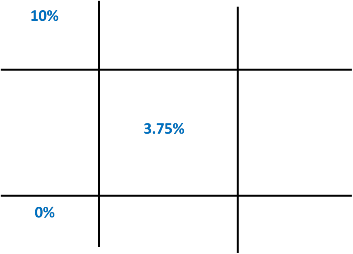
Now, subtract diagonally to determine parts of the 10% zinc oxide ointment and ointment base needed.
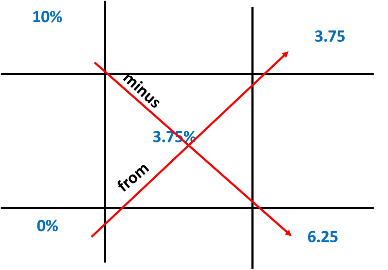
The total parts are equal to 3.75 + 6.25 or 10. The ratio and proportion method can be used to determine the quantities of the 10% zinc oxide ointment and ointment base that are needed as follows.
10% zinc oxide ointment
3.75 parts/x grams = 10 parts/120 grams x = 45 grams 10% zinc oxide ointment
Ointment base
6.25 parts/x grams = 10 parts/120 grams x = 75 grams ointment base
Check it Out!
45 grams + 75 grams = 120 grams, which is the total mentioned in the problem. This is a good initial indication that the problem has been solved correctly. We can further check our work by determining that 45 grams of a 10% zinc oxide ointment will contain 4.5 grams of zinc oxide (45 x 0.10). 4.5 grams in a total of 120 grams of ointment yields a 3.75% ointment.
Calculations for Reconstitution
Many drugs lose potency when they are prepared in a liquid dosage form and need to be provided as dry powders to extend shelf lives.2 These products then need to be reconstituted with purified water to prepare them in a liquid dosage form.2,3 Typically, these products can be reconstituted by following instructions to add the correct amount of purified water or diluent to achieve the intended concentration. The final volume of the preparation is the sum of the diluent and volume occupied by the powder.2,3 Compounding personnel may need to adjust the concentration of the medication based on the prescriber’s recommendation.
Compounding personnel should be familiar with the equation for powder volume, which is the volume occupied by dry powder in a container. This equation can also be rearranged to solve for the final volume of a preparation.
Powder volume = final volume – diluent volume
Final volume = diluent volume + powder volume
Example: The label for a dry powder package of an antibiotic for oral suspension says to add 84 mL of purified water to make 100 mL of suspension. The package contains 2 grams of the antibiotic. Calculate the volume represented by the suspended powder in the product.
To solve, use the powder volume equation. The final volume of the product per the problem is 100 mL. The volume of diluent added is 84 mL.
Powder volume = final volume – diluent volume Powder volume = 100 mL – 84 mL
Powder volume = 16 mL
Example: If a physician desires a new concentration of antibiotic of 125 mg/5 mL, how many milliliters of water should be added to the dry powder?
From the previous problem, we know there are 2 g or 2000 mg of the antibiotic within the container. This total can be used to calculate the total volume needed for a concentration of 125 mg/5 mL using the ratio and proportion method:
2000 mg/x mL = 125 mg/5 mL = 80 mL
The dry powder occupies 16 mL. This value can be put into the powder volume equation to determine the necessary amount of diluent.
Diluent volume = 80 mL – 16 mL = 64 mL
Take-home message:
One of many resources for practice and reference is the Master Pharmacy Calculations. Pharmafactz. 2023 https://pharmafactz.com/pharmacy-calculations/
Summary
Understanding pharmaceutical calculations is important to ensure accuracy when compounding. Compounding personnel should be familiar with calculations involving ratios/proportions, dimensional analysis, expressions of concentration, density, and specific gravity. They should also be able to use the aliquot method and alligation method and complete calculations for dosing and reconstitution of powders.
Course Test
One pound (lb.) equals how many grams (g.)?
16 grams
100 grams
254 grams
454 grams
Two pints (pt.) equals how many milliliters (mL)?
30 mL
96 mL
546 mL
946 mL
Which of the following equations can be used to solve for powder volume?
Powder volume = final volume – diluent volume
Powder volume = diluent volume – final volume
Powder volume = quantity of solute/quantity of preparation
Powder volume = volume of preparation – volume of solute
Which of the following equations can determine the least weighable quantity (LWQ)?
LWQ = %error tolerated/sensitivity requirement x 100%
LWQ = sensitivity requirement/%error tolerated x 100%
LWQ = 100 x sensitivity requirement + %error tolerated
LWQ = %error tolerated/100
The specific gravity of white petrolatum is 0.850. At what weight will this substance fill an ointment jar with a capacity of one fluid ounce (1 fl. oz = 30 mL)?
12.8 grams
25.5 grams
30 grams
30.6 grams
If 12 grams of lanolin are combined with 2 grams of white wax and 16 grams of petrolatum to make an ointment, what is the w/w percentage concentration of lanolin in this preparation?
10% w/w
20% w/w
40% w/w
80% w/w
Convert 0.4% v/v to a ratio strength.
1:100
1:250
1:500
1:550
What is the least weighable quantity of a balance with a sensitivity requirement of 4 mg and a percent error tolerated of 3%?
100 mg
120 mg
133 mg
150 mg
How many grams of an 8% progesterone gel should be added to
1.5 grams of a 4 percent progesterone gel to make a 5% progesterone gel?
0.5 grams
1 gram
2.5 grams
5 grams
The label for a dry powder package of an antibiotic for oral suspension says to add 75 mL of purified water to make 100 mL of suspension. The package contains 1500 grams of the antibiotic. Calculate the volume represented by the suspended powder in the product.
25 mL
50 mL
75 mL
100 mL
References
General Chapter: USP. Pharmaceutical Compounding-Nonsterile Preparations <795>. In: USP-NF. Rockville, MD: USP; September 2022.
Teixeira M, Zatz J. Pharmaceutical Calculations. 5th ed. Wiley. 2017
Ansel H and Stockton S. Pharmaceutical Calculations. 15th edition. LWW. 2016.
DISCLAIMER
The information provided in this course is general in nature, and it is solely designed to provide participants with continuing education credit(s). This course and materials are not meant to substitute for the independent, professional judgment of any participant regarding that participant’s professional practice, including but not limited to patient assessment, diagnosis, treatment, and/or health management. Medical and pharmacy practices, rules, and laws vary from state to state, and this course does not cover the laws of each state; therefore, participants must consult the laws of their state as they relate to their professional practice.
Healthcare professionals, including pharmacists and pharmacy technicians, must consult with their employer, healthcare facility, hospital, or other organization for guidelines, protocols, and procedures they are to follow. The information provided in this course does not replace those guidelines, protocols, and procedures but is for academic purposes only, and this course’s limited purpose is for the completion of continuing education credits.
Participants are advised and acknowledge that information related to medications, their administration, dosing, contraindications, adverse reactions, interactions, warnings, precautions, or accepted uses are constantly changing, and any person taking this course understands that such person must make an independent review of medication information prior to any patient assessment, diagnosis, treatment and/or health management. Any discussion of off-label use of any medication, device, or procedure is informational only, and such uses are not endorsed hereby.
Nothing contained in this course represents the opinions, views, judgments, or conclusions of RxCe.com LLC. RxCe.com LLC is not liable or responsible to any person for any inaccuracy, error, or omission with respect to this course, or course material.
© RxCe.com LLC 2023: All rights reserved. No reproduction of all or part of any content herein is allowed without the prior, written permission of RxCe.com LLC.